Расчет сопротивления движения поезда, расхода и стоимости электроэнергии на движение поезда

Какие факторы могут изменить коэффициент сопротивления движению?

1. Форма тела: Геометрическая форма тела оказывает большое влияние на его коэффициент сопротивления. Сферическое тело имеет меньший коэффициент сопротивления, чем тело с вытянутой формой, так как форма сферы способствует более плавному движению.

2. Площадь поперечного сечения: Площадь поперечного сечения тела также влияет на его коэффициент сопротивления. Чем больше площадь поперечного сечения, тем больше сопротивление воздуха и, соответственно, больше коэффициент сопротивления.

3. Состояние поверхности: Состояние поверхности тела также может изменить его коэффициент сопротивления. Гладкая поверхность имеет меньший коэффициент сопротивления, чем шероховатая поверхность. Потому что шероховатости создают дополнительные завихрения и трение воздуха, что в свою очередь приводит к увеличению сопротивления.

4. Плотность среды: Коэффициент сопротивления может изменяться в зависимости от плотности среды, через которую движется тело. Чем больше плотность среды, тем больше сопротивление движению и, следовательно, больше коэффициент сопротивления.

5. Скорость движения: Скорость движения тела также оказывает влияние на его коэффициент сопротивления. Обычно, с увеличением скорости коэффициент сопротивления растет.

6. Температура среды: Температура среды может изменять вязкость и плотность среды, что в свою очередь влияет на коэффициент сопротивления. При повышении температуры, воздух становится менее плотным, и коэффициент сопротивления уменьшается.

Динамика прямолинейного движения

Пример HTML-страницы

Общее сопротивление движению

Сопротивление движению вычисляется как (рис. «Силы сопротивления движению» ):

F_W=F_Ro + F_L+F_St

Мощность, которая должна поступить на ве­дущие колеса автомобиля для преодоления сопротивления движению (силы сопротивле­ния движению), равна:

P_W = F_W v или P_W = F_WV /3600

где:

 P_w в кВт,

F_w в Н,

v в км/ч.

Сопротивление качению

Сопротивление качению является следствием возникающих процес­сов деформации в зоне контакта шины с до­рогой. При этом применимо следующее:

Fro =f G cosa — fmg cosa

Приближенный расчет сопротивления каче­нию может быть выполнен путем использо­вания коэффициентов, представленных в приведенной ниже таблице  «Коэффициенты сопротивления качению» и на рис. «Сопротивление качению радиальных шин по ровной, горизонтальной дороге при нормальных нагрузке и внутреннем давлении».

Увеличение коэффициента сопротивления качению f прямо пропорционально уровню деформации и обратно пропорционально ра­диусу шины. Следовательно, коэффициент будет увеличиваться при увеличении нагрузки, скорости и при снижении давления в шине.

При прохождении поворотов сопротивле­ние качению увеличивается за счет добавоч­ного сопротивления повороту:

F_k=f_кG

Коэффициент сопротивления повороту f_кявляется функцией скорости движения авто­мобиля, радиуса поворота, геометрических характеристик подвески автомобиля, типа шин, давления в шинах и поведения автомо­биля под действием поперечного ускорения.

Таблица.«Коэффициент аэродинамического сопротивления и мощность, затрачиваемая на преодоление аэродинамического сопротивления, для различных типов кузова»

Аэродинамическое сопротивление

Определяется по формуле:

F_L = 0,5 p⋅ c_w⋅ А (v + v)2 

или

F_L =0,0386⋅ р⋅ c_w⋅ А (v + v)2,

где: v в км/ч, F_L в Н, р в кг/м3, А в м2, плотность воздуха р = 1,202 кг/м3 на высоте 200 м.

Аэродинамическое сопротивление:

P_L = F_L = 0,5 р c_w Av (v + v)2 

или

P_L = 12,9-10-6 c_w A v (v + v)2

где: P_L в кВт, F_L в Н, v и v в км/ч, А в м2, р = 1,202 кг/м3.

Максимальное поперечное сечение автомобиля: А ≈0,9 х ширина колеи х высота.

Пример HTML-страницы

Автомобиль движется накатом на нейтральной передаче в условиях безветрия по ровной до­роге. Для двух заданных значений скоростей движения, v₁ (высокая скорость) и v₂ (малая скорость), замеряется время, необходимое, чтобы автомобиль при этих условиях замед­лил свое движение. Эта информация исполь­зуется для расчета средних замедлений a₁ и а₂. Формулы и примеры из табл. «Эмпирические определения коэффициентов аэродинамического сопротивления и сопротивления качению» приведены для автомобиля массой m = 1450 кг с площадью поперечного сечения А = 2,2 м2 .

Этот метод применим для скоростей дви­жения автомобиля до 100 км/ч.

Сопротивление движению на подъем (F_st со знаком плюс) и силы, действующие на автомо­биль при движении под уклон (F_st со знаком минус) рассчитываются следующим образом:

F_st = G sinа = m g sina

или приближенно:

F_st ≈ 0,01 m g p

Эти уравнения применимы с уклонами до р ⩽ 20%, поскольку при малых углах применимо следующее:

sina ≈ tana (погрешность менее 2 %).

Мощность, затрачиваемая на преодоление подъема, равна:

P_st = F_st v   или  если P_st измеряется в кВт, F_st в Н и v в км/ч:

P_st = F_st v/3600 = m g v sina/3600

или приближенно:

_Pst = m g p v / 3600

Продольный уклон дороги равен:

р = (h/l)⋅100 % или р = (tanа) ⋅100 %

где h соответствует проекции наклонной поверхности l на вертикальную ось.

В англоязычных странах продольный уклон определяется отношением 1 в 100/р .

Например, при р =50% отношение 1 к 2.

Пример вычисления силы тяги и мощности, затрачиваемой на преодоление подъема

Пример HTML-страницы

Для преодоления подъема с уклоном р = 21 %, автомобилю массой 1500 кг потре­буется сила тяги на колесах приблизительно 1,5 x 2000 Н = 3000 Н (значение из табл. «Угол уклона и сопротивление движению на подъем» ) и при v = 40 км/ч мощность, затрачиваемая на преодоление подъема, приблизительно 1,5 х 22 кВт = 31 кВт (значение из табл. «Сопротивление движению на подъем и мощность, затрачиваемая на преодоление подъема» ).

Сила тяги

Чем больше крутящий момент двигателя М и общее передаточное число трансмиссии i между двигателем и ведущими колесами, и чем ниже потери мощности в трансмиссии, тем выше сила тяги F на ведущих колесах автомобиля.

F = (Mi/r)⋅η  или F = P η / v

η — КПД привода. Для двигателя про­дольного расположения η ≈ 0,88 — 0,92, для двигателя поперечного расположения η ≈0,91 -0,95.

Сила тяги частично затрачивается на преодо­ление сопротивления движению. При боль­шом сопротивлении движению, имеющем место на подъемах, следует включать в ко­робке передач пониженную передачу (т. е. увеличивать передаточное число трансмис­сии).

Формула для вычисления пути

Для вычисления пути, пройденного телом при известной скорости и коэффициенте трения, можно использовать следующую формулу:

Путь = (Скорость2 / (2 * Коэффициент_трения * Ускорение_свободного_падения)

В этой формуле:

• Скорость — скорость тела, с которой оно движется;
• Коэффициент_трения — безразмерное количество, которое определяет силу трения между телом и поверхностью;
• Ускорение_свободного_падения — ускорение, равное 9,8 м/с2 на Земле.

Очень важно учесть, что эта формула применима только в случае постоянной скорости и постоянного коэффициента трения. Если эти условия не соблюдаются, результаты могут быть неточными

Влияние массы тела на коэффициент трения и скорость движения

Масса тела является одним из ключевых факторов, определяющих его скорость движения и влияние на коэффициент трения между телом и поверхностью.

Физический закон, лежащий в основе данного влияния, заключается в том, что трение между телами возникает в результате взаимодействия молекул поверхности и молекул тела. Трение возникает только при движении тела по поверхности, и его сила пропорциональна нормальной силе, действующей на тело в результате его веса.

С увеличением массы тела, нормальная сила также увеличивается, что ведет к увеличению силы трения. Таким образом, при большей массе тела трение между телом и поверхностью будет сильнее, что может сказаться на скорости его движения.

Однако, следует отметить, что влияние массы на скорость движения также зависит от других факторов, таких как коэффициент трения, сила тяги, сопротивление воздуха и т.д. Например, при движении тела по горизонтальной поверхности с постоянной силой тяги, увеличение массы тела будет сопровождаться уменьшением его ускорения и, следовательно, скорости. Это связано с тем, что сила трения увеличивается пропорционально нормальной силе, действующей на тело.

Таким образом, для того чтобы определить влияние массы на скорость движения тела, необходимо учитывать не только массу самого тела, но и другие факторы, влияющие на движение тела, такие как коэффициент трения, сила тяги, сопротивление воздуха и другие внешние силы.

От чего зависит сопротивление качению

На качение влияют разные факторы. Значительная часть относится к особенностям самой шины и ее состоянию:

1. Конструкция и материалы. Влияют на степень деформации в пятне контакта и трение с дорожным покрытием.
2. Индекс скорости. Некоторые решения, направленные на повышение курсовой устойчивости, негативно сказываются на экономичности.
3. Сезонность. Зимние шины («липучки») должны обеспечивать максимальное сцепление с мокрой и скользкой дорогой, и они априори не могут быть более экономичными чем летние.
4. Посадочный диаметр и высота профиля. Чем больше общий диаметр колеса, тем ниже сопротивление качению.
5. Рисунок протектора. Мелкий и глубокий рисунок увеличивает аэродинамическое сопротивление покрышки. «Лысые» старые шины катятся лучше, чем новые.
6. Давление. Чем ниже давление в шине, тем выше сопротивление качению.

На качение влияют и внешние факторы. К ним относятся:

1. Тип дорожного покрытия. У бетонки и брусчатки сопротивление больше, чем у асфальта. Мягкая грунтовка немного продавливается и «пылит» под тяжестью автомобиля, что увеличивает расход топлива. На щебенке без битумной пропитки колеса пробуксовывают.
2. Качество дорожного покрытия. Шероховатая структура, ухабы, ямы, колея — все это мешает движению.
3. Температура покрытия. От 10°C до 40°C сопротивление качению снижается, а затем — растет.

Задачи на Движение под действием силы трения

Тренировочные задания для подготовки к контрольным,
самостоятельным и диагностическим работам по теме
«ЗАДАЧИ на Движение под действием силы трения» + Решения

Модуль силы трения скольжения можно определить по формуле: F_тр = µN, где µ — коэффициент трения, N— модуль силы нормального давления (и силы реакции опоры). Максимальная сила трения покоя: (F_тр)_мах = µN. При одинаковых условиях сила трения скольжения намного больше силы трения качения. Вектор силы трения скольжения всегда направлен противоположно вектору скорости тела. Коэффициент трения можно определить по формуле: µ = F_тр/N. Это величина безразмерная.

Если на тело действует только сила трения, то такое тело движется равнозамедленно до остановки. Расстояние, которое тело проходит до остановки, называют тормозным путем. Обозначают буквой l. Время торможения — время, нужное для остановки.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
Автомобиль массой 5 т движется с постоянной скоростью по прямой горизонтальной дороге. Коэффициент трения шин о дорогу равен 0,03. Определите силу тяги, развиваемую двигателем.

ОТВЕТ: F_тяги = 1470 Н.

РЕШЕНИЕ:

Задача № 2.
Сани со стальными полозьями перемещают равномерно по льду, прилагая горизонтальное усилие 2 Н. Каков вес саней?

ОТВЕТ: Вес саней 100 Н.

Задача № 3.
Деревянный брусок массой 3 кг тянут по горизонтальной деревянной доске с помощью пружины. Коэффициент трения равен 0,3. Найти удлинение пружины, если ее жесткость 10 кН/м.

ОТВЕТ: Удлинение пружины 0,09 см.

Задача № 4.
Велосипедист, ехавший со скоростью 36 км/ч, увидел примерно в 10 м от себя препятствие и резко затормозил. Успеет ли велосипедист остановиться до препятствия?

ОТВЕТ: Велосипедист успеет остановиться до препятствия, так как S = 10 м (расстояние до препятствия), а тормозной путь велосипедиста ≈ 7 м. Если скорость движения возрастет вдвое, то тормозной путь увеличится в 4 раза.

Задача № 5.
Автомобиль движется со скоростью 10 м/с по гладкой горизонтальной дороге. Пройдя с выключенным мотором расстояние 150 м, автомобиль останавливается. Сколько времени автомобиль двигался с выключенным мотором и каков коэффициент трения при его движении?

ОТВЕТ: t = 30 с;  µ = 0,033.

ЗАДАЧИ на Движение под действием силы трения

Задача № 6.
Лыжник массой 60 кг, имеющий в конце спуска скорость 10 м/с, останавливается через 40 с после окончания спуска. Определить величину силы сопротивления.

ОТВЕТ: F_тp = 15 Н.

Задача № 7.
Тело скользит равномерно по наклонной плоскости с углом наклона 30°. Определите коэффициент трения тела о плоскость.

ОТВЕТ: µ ≈ 0,58.

Задача № 8.
С какой наибольшей скоростью может ехать мотоциклист по горизонтальной плоскости, описывая дугу радиусом 80 м, если коэффициент трения резины о почву 0,4? На какой угол от вертикального положения он при этом отклоняется?

ОТВЕТ: v_мах = 17,7 м/с = 64 км/ч — наибольшая скорость движения; a ≈ 22°.

Задача № 9.
Шофер грузовика, едущего со скоростью 72 км/ч, заметил на дороге знак. Сможет ли он, не сбавляя скорости, проехать поворот, если его радиус равен 25 м? Считать коэффициент трения шин о дорогу 0,4.

ОТВЕТ: Шофер должен уменьшить скорость движения, так как радиус окружности, которую опишет грузовик при данной скорости, 100 м, а радиус поворота — 25 м. В противном случае грузовик занесет на обочину дороги.

Дополнительный материал для решения задач

Конспект урока по физике «ЗАДАЧИ на Движение под действием силы трения с решениями». Тренировочные задания для подготовки к контрольным, самостоятельным, проверочным и диагностическим работам. Выберите дальнейшее действие:

• Вернуться к Списку конспектов по физике для 7-11 классов
• Найти конспект через Кодификатор ОГЭ по физике
• Найти конспект через Кодификатор ЕГЭ по физике

Проработанные примеры

Давайте рассмотрим несколько примеров, чтобы понять, как рассчитать сопротивление воздуха в различных сценариях:

Пример расчета сопротивления воздуха в физике

Представьте себе небольшой металлический шарик, свободно падающий в воздухе. Шар имеет массу 0.1 кг и диаметр 0.05 метра. Плотность воздуха 1.2 кг/м³. Определите сопротивление воздуха, действующее на мяч, когда его скорость равна 10 м/с.

Данный:
— Масса шара (м) = 0.1 кг.
— Диаметр шара (d) = 0.05 м.
– Плотность воздуха

Сначала нам нужно вычислить опорную площадь (А) шара. Поскольку это сфера, эталонная площадь определяется по формуле:

Подставив значения, получим:

Далее мы можем рассчитать сопротивление воздуха по уравнению:

Приняв коэффициент сопротивления (C_d) небольшого металлического шарика равным 0.47, мы можем заменить значения:

Следовательно, сопротивление воздуха, действующее на шар, составляет примерно 0.1135 Ньютона.

Пример расчета сопротивления воздуха на выпускном экзамене по физике

Учащийся проводит эксперимент по определению сопротивления воздуха различной формы. Они бросают куб, сферу и плоский диск с одинаковой высоты и измеряют время, необходимое каждому предмету, чтобы достичь земли. Масса куба 0.2 кг, масса шара 0.3 кг, масса диска 0.15 кг. Высота падения — 5 метров, а плотность воздуха — 1.2 кг/м³. Рассчитайте сопротивление воздуха для каждого объекта, используя измеренное время и уравнение сопротивления воздуха.

Данный:
– Масса куба (m_cube) = 0.2 кг.
– Масса сферы (m_sphere) = 0.3 кг.
– Масса диска (m_disc) = 0.15 кг.
– Высота падения (h) = 5 м
– Плотность воздуха

Предположим, что время, необходимое кубу для достижения земли, составляет 2.5 секунды, время, необходимое для сферы, — 3 секунды, а время, необходимое для диска, — 2 секунды.

Сначала рассчитаем скорость каждого объекта по формуле:

Для куба:

Для сферы:

Для диска:

Далее мы вычисляем эталонную площадь (А) для каждого объекта.

Предполагая, что куб, сфера и диск имеют длину сторон 0.1 м, диаметр 0.15 м и 0.2 м соответственно, эталонные площади будут следующими:

Для куба:

Для сферы:

Для диска:

Наконец, мы можем рассчитать сопротивление воздуха для каждого объекта, используя уравнение:

Приняв коэффициент сопротивления (C_d) равным 0.5 для всех объектов, мы можем подставить значения и рассчитать сопротивление воздуха:

Для куба:

Для сферы:

Для диска:

Следовательно, сопротивление воздуха для куба составляет примерно 0.024 Ньютона, для сферы — примерно 0.022 Ньютона, а для диска — примерно 0.081 Ньютона.

Пример расчета сопротивления воздуха при движении снаряда

Мяч брошен с начальной скоростью 15 м/с под углом 30 градусов к горизонту. Масса шара 0.2 кг, плотность воздуха 1.25 кг/м³. Определите сопротивление воздуха, действующее на мяч во время его полета.

Данный:
– Начальная скорость мяча (v) = 15 м/с.
— Угол запуска (θ) = 30 градусов
— Масса шара (м) = 0.2 кг.
– Плотность воздуха

Для расчета сопротивления воздуха во время полета мяча необходимо рассматривать отдельно его горизонтальную и вертикальную составляющие.

Для горизонтальной составляющей скорость остается постоянной, и в этом направлении сопротивление воздуха не действует.

Что касается вертикальной составляющей, сопротивление воздуха препятствует движению, влияя на траекторию мяча.

Сначала рассчитаем вертикальную скорость (v_vertical) по формуле:

Подставив данные значения, получим:

Далее вычисляем опорную площадь (А) шара. Предполагая, что шар имеет сферическую форму и диаметр 0.1 метра, базовая площадь определяется как:

Наконец, мы можем рассчитать сопротивление воздуха, используя уравнение:

Предполагая, что коэффициент сопротивления (C_d) для мяча равен 0.45, мы можем заменить значения:

Следовательно, сопротивление воздуха, действующее на шарик во время его полета, составляет примерно 0.081 Ньютона.

Расчет сопротивления воздуха важен для понимания влияния сопротивления на движущиеся объекты. Применяя базовое уравнение, учитывая переменные и следуя шагам, описанным в этом сообщении блога, вы можете точно рассчитать сопротивление воздуха в различных сценариях. Независимо от того, изучаете ли вы физику, инженерное дело или просто интересуетесь силами, действующими в окружающем нас мире, освоение расчета сопротивления воздуха расширит ваше понимание и позволит вам принимать более обоснованные решения в практических приложениях. Итак, в следующий раз, когда вы увидите объект, движущийся в воздухе, помните, что сопротивление воздуха, которое он испытывает, можно измерить и проанализировать, используя концепции и методы, обсуждаемые здесь.

Методы снижения коэффициента сопротивления

1. Оптимизация формы и профиля

Изменение формы и профиля объекта может значительно снизить коэффициент сопротивления движению. При проектировании автомобилей, самолетов и других транспортных средств учитывается аэродинамика, с целью снижения сопротивления воздуха. Углы наклона, радиусы закругления, крылья и другие детали конструкции предусматриваются с учетом минимизации сопротивления движению.

2. Использование современных материалов

Современные материалы с низким коэффициентом трения позволяют снизить сопротивление движению. В автомобильной и авиационной индустрии используются специальные композитные материалы, которые обладают легкостью и прочностью, а также способностью снижать сопротивление воздуха. Это позволяет улучшить эффективность и экономичность работы транспортных средств.

3. Внедрение новых технологий

Применение новых технологий таких, как умные системы управления и мультимедиа, позволяет оптимизировать работу двигателя в режиме экономии топлива. Многие автомобили и самолеты оснащаются системами автоматического управления, которые контролируют работу двигателя и других систем для снижения сопротивления движению и повышения эффективности.

4. Улучшение шин и колесных дисков

Шины и колесные диски также играют важную роль в снижении сопротивления движению. Низкопрофильные шины с меньшим коэффициентом трения и аэродинамические формы колесных дисков помогают улучшить общую эффективность транспортного средства. Правильный выбор шин и колесных дисков может существенно снизить сопротивление движению и повысить экономичность.

5. Методы снижения веса

Уменьшение массы объекта также способствует снижению сопротивления движению. Чем легче объект, тем меньше энергии требуется для его перемещения. Применение легких материалов, оптимизация конструкции и использование новых технологий позволяют уменьшить вес транспортного средства и снизить коэффициент сопротивления движению.

Основные принципы определения скорости с помощью коэффициента трения

Определение скорости движения тела с использованием коэффициента трения основано на изучении силы трения между телами. Коэффициент трения позволяет определить, с какой силой тело тормозится или движется по горизонтальной поверхности.

Основной принцип, на котором основано определение скорости с помощью коэффициента трения, заключается в равенстве силы трения и силы, вызывающей движение:

Сила трения = Сила движения

При наличии равенства этих сил можно определить скорость, с которой тело движется или тормозится.

Существуют два основных типа трения — сухое и жидкостное трение. Сухое трение возникает при движении твердых тел по поверхности, а жидкостное трение — при движении тел в жидкой среде. Для определения скорости с помощью коэффициента трения, необходимо знать коэффициент трения данной поверхности.

Коэффициент трения определяется экспериментально и зависит от множества факторов, включая природу поверхности и состояние тела. Например, для сухого трения этот коэффициент может изменяться в зависимости от состояния поверхности (сухой или мокрый асфальт), а для жидкостного трения — от вязкости жидкости и формы тела.

Определение скорости с использованием коэффициента трения может выполняться различными способами, включая использование формул, таблиц и графиков. Для этого необходимо учитывать все факторы, влияющие на трение и скорость движения тела.

Пример определения скорости с использованием коэффициента трения:

Допустим, у нас есть тело массой 2 кг, которое движется по горизонтальной поверхности с коэффициентом трения 0,3. Расстояние, которое тело пройдет до полной остановки, составляет 10 метров. Мы хотим определить начальную скорость этого тела. Для этого мы можем использовать формулу:

1. Определим силу трения с помощью формулы: Сила трения = Масса × Ускорение
2. Используем формулу для определения ускорения: Ускорение = Сила трения / Масса
3. Подставим известные значения в формулу и найдем ускорение
4. Используем формулу для определения начальной скорости: Начальная скорость = Корень квадратный из (2 × Ускорение × Расстояние)
5. Вычислим начальную скорость с использованием известных значений

Таким образом, мы можем определить начальную скорость тела, используя коэффициент трения и другие известные параметры.

Практическое применение знаний о коэффициенте трения для определения скорости

Знание о коэффициенте трения является важным для различных прикладных областей, связанных с определением скорости.

• Дорожное движение: Знание коэффициента трения между шиной автомобиля и дорожным покрытием позволяет определить расстояние торможения и безопасную скорость движения на различных дорожных условиях.
• Спортивные соревнования: Например, в беге на короткие дистанции знание коэффициента трения между беговыми ботинками и поверхностью дорожки позволяет спортсменам выбрать наиболее подходящие и эффективные обувь и поверхность для достижения максимальной скорости.
• Аэродинамика: Коэффициент трения летательных аппаратов с воздушной средой может быть использован для оценки их аэродинамических характеристик, таких как лобовое сопротивление и скорость полета.
• Промышленные процессы: Коэффициент трения может быть использован для оптимизации дизайна и производства различных механизмов и машин, таких как конвейеры и транспортные ленты, чтобы достичь оптимальной скорости и эффективности работы.

Во всех этих практических примерах знание о коэффициенте трения позволяет предсказывать и оптимизировать скорость движения и работы различных систем, что является важным для повышения безопасности, эффективности и производительности.

Момент и коэффициент

Пусть имеется цилиндр, расположенный на идеальной гладкой жёсткой поверхности. Какую бы силу Q ни приложили, уравновесить её можно только противодействующей энергией. Если же такой энергии нет, под действием Q цилиндр должен катиться. Но опыты показывают совершенно другое. Например, если подойти к многотонному грузовику и попробовать его толкнуть, он не покатится. Хотя теория утверждает обратное.

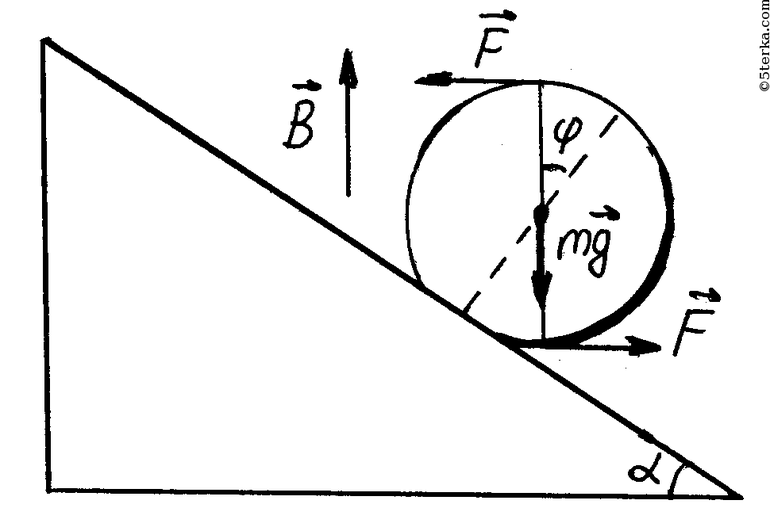
Но здесь дело в том, что поверхность считается идеальной. В момент времени на тело, кроме Q, действует равное ей сцепление. Эти силы будут уравновешенными. В вертикальной же плоскости на тело действует нормаль (N) и противодействующая ей сила равновесия (P).

На самом деле при прикосновении тело деформируется. Образуется впадина, при этом колесо всей своей тяжестью будет опираться на крайнюю правую точку деформированной поверхности. Момент сил здесь будет следующим:

• P — вес колеса, направленный вниз;
• N — момент нормали противоположный P;
• Q — импульс качения.

Перемещению препятствует равновесие пары PN. При этом плечо пары будет половиной размера, то есть возникает момент сил трения. Определяют его как эн делённое на дельту и называют моментом трения: Mтр = N * d. Эта формула совпадает по форме записи с законом Амонтона — Кулона. И там, и тут фигурирует величина опоры.

Становится очевидным, что R * Q = Mтр = P * d. Используя эту запись, можно обнаружить предельный импульс, который необходимо приложить к колесу, чтобы заставить его двигаться: Q = p d /R. При этом если колесо будет скользить, а не катиться, Q будет уже зависеть от трения: Q = P * f.

При сравнении двух формул видно, что d / r будет намного меньше f, поэтому качение произойдёт раньше. Это свойство как раз и используется в подшипниках. Нахождение коэффициента трения можно выполнить через момент трения качения и давление прижима: f = Mтр / N.

Он определяется следующими физическими интерпретациями:

• f равна длине линии, соединяющей прямые, вдоль которых создаются нормаль и давление вниз;
• для неидеализированных случаев мгновенный центр вращения сдвинут в сторону качения тела, при этом значение смещения равно коэффициенту трения.

Формула силы тока и сопротивление

Формула 6

Законом Ома для участка цепи называют взаимосвязь между силой тока (I), напряжением (U) и сопротивлением (R) проводника на практике установлена Г. Омом.

\

Материалы с низким удельным сопротивлением считаются проводниками, они эффективно проводят электрический ток. С высоким удельным сопротивлением – диэлектрики, их используют как изоляторы. Промежуточное положение занимают полупроводники.

Пример

Найти силу тока в проводнике длиной 100 мм, сечением 0,5 мм2 изготовленном из меди, если напряжение на его концах 6,8 В.

Решение:

Запишем формулу закона Ома и найдем сопротивление через силу тока : \

Для определения силы тока I, нужно определить сопротивление R. С помощью формулы с удельным сопротивлением преобразуем формулу для закона Ома:

\

Подставляем значения в формулу:

\

Значение ρ для меди берется из таблиц.

Ответ: 2А