Измерение фи в физике электричества

Фи в движении по окружности: принцип работы и приложение

Основной принцип работы фи основан на использовании магнитных полей. Микроробот приводится в движение с помощью внешних магнитных полей, которые передаются через покрытие из магнитных наночастиц. Это позволяет управлять движением фи с точностью до нескольких микрометров.

Фи имеет широкое применение в медицинской сфере. Благодаря своим малым размерам, этот микроробот может использоваться для доставки лекарственных препаратов в определенные участки организма. Фи способен проникать в труднодоступные места, такие как опухоли или большие сосуды, и доставлять лекарство прямо на место воздействия.

Кроме того, фи может использоваться для биопсии или диагностики. Наносистема с камерой, расположенной на спине микроробота, позволяет получать изображения и передавать их на внешний устройство. Таким образом, можно проводить точные и малоинвазивные исследования внутренних органов и тканей пациента.

Применение фи также затрагивает область нанотехнологий. Микроробот может использоваться для создания трехмерных структур путем точного размещения материалов с на малых масштабах. Это может быть полезно, например, для создания определенных микрочипов или биоорганических конструкций.

В целом, фи в движении по окружности открывает новые перспективы в робототехнике и медицине. Своей программируемой системой и точностью управления он предоставляет широкие возможности для различных приложений, что делает его одним из самых перспективных разработок в этой области.

Единицы измерения ФИ

В физике величину ФИ обозначают буквой Ф. Она представляет собой магнитный поток, который проходит через некоторую поверхность. Магнитный поток – это величина, которая характеризует количество магнитных полей, проходящих через данную поверхность.

ФИ является переменной величиной и измеряется в единицах магнитного потока, называемых веберами (Вб). Один вебер соответствует одному магнитному потоку, проникающему через поверхность, равную площади 1 квадратного метра, под прямым углом к магнитной индукции.

Магнитная индукция – это векторная величина, которая характеризует силу и направление магнитного поля. Она измеряется в теслах (Тл) или в гауссах (Гс). Единица тесла соответствует одной вебер в плоскости 1 квадратного метра, а единица гаусса равна 10-4 теслам.

Кроме того, в физике используется также понятие работы магнитной индукции. Работа магнитной индукции – это энергия, которая затрачивается на перемещение заряда в магнитном поле. Она измеряется в джоулях (Дж).

Единицы измерения ФИ и связанных величин

Величина
Единица измерения

ФИ (магнитный поток)
Вебер (Вб)

Магнитная индукция
Тесла (Тл), Гауссы (Гс)

Работа магнитной индукции
Джоуль (Дж)

Таким образом, ФИ, магнитная индукция и работа магнитной индукции – это важные понятия в физике, которые позволяют описать электрическую и магнитную природу материи и являются основой для измерения и расчетов в данной области.

Примеры использования ФИ

В физике величина ФИ обозначает фазу или угол, который характеризует положение вектора или волновой функции.

Например, в классической механике для описания кругового движения используется величина ФИ, которая представляет собой угол, пройденный телом.

Также величина ФИ связана с электромагнитным полем. Например, электрическое поле описывается множеством силовых линий, а каждая силовая линия имеет свою угловую координату ФИ, указывающую направление электрического поля в конкретной точке пространства.

ФИ также используется для описания магнитного поля. Например, можно представить магнитное поле как множество силовых линий, где каждая линия имеет свою угловую координату ФИ.

Величина ФИ также применяется к переменным полям. Например, величина ФИ может быть использована для описания изменений уровня электрического или магнитного поля с течением времени.

Роль буквы ФИ в измерениях

Магнитный поток связан с магнитным моментом тела и его механическим и магнитным свойствами. Чтобы измерить магнитный поток, используется специальная величина — ФИ.

ФИ обычно выражается в веберах (Вб) — единицах магнитного потока. Магнитный поток также может быть измерен в гауссах (Гс) или теслах (Тл), в зависимости от системы измерений.

Магнитный поток может быть связан с магнитной индукцией B, которая показывает магнитное поле в определенной точке. ФИ и B связаны уравнением ФИ = B * S * cos(α), где S — площадь поверхности, через которую проходит магнитный поток, а α — угол между вектором нормали к поверхности и вектором магнитной индукции.

ФИ также может быть связана с электрическими величинами. Например, с помощью закона Фарадея можно измерять магнитный поток, используя электрическое поле и изменение магнитного потока. Также магнитный поток может вызывать электрическую силу — эффект Магнуса, который используется в различных приборах и технологиях.

Таким образом, буква ФИ играет ключевую роль в измерениях магнитного потока, связывая его с различными физическими величинами, такими как магнитная индукция, электрическое поле и сила. Это позволяет ученым и инженерам изучать и использовать магнитное поле и его свойства в различных областях, таких как электродинамика, электрическая и магнитная техника и другие.

Значение ФИ в точности измерений

Величины физических величин измеряются с использованием различных инструментов и приборов, таких как весы, штангенциркуль, электромагниты и другие. Каждая величина имеет свои собственные единицы измерения, которые помогают определить ее значимость и влияние на процесс измерения.

Необходимо учитывать, что точность измерения может быть ограничена различными факторами, такими как погрешность измерительного прибора, погрешность среды, в которой проводятся измерения, и другие

Поэтому важно правильно оценить и учесть все факторы, которые могут повлиять на точность измерений

Физическая величина	Значение	Единица измерения
Сила	Воздействие, способное изменить состояние движения или формы тела.	Ньютон (Н)
Индукция	Распределение физической величины в пространстве.	Тесла (Тл)
Механическое момент	Физическая характеристика вращающегося объекта.	Ньютон-метр (Н·м)
Электрическая индукция	Физическая характеристика электрического поля.	Кулон на квадратный метр (Кл/м²)
Магнитная индукция	Физическая характеристика магнитного поля.	Тесла (Тл)
Электрический момент	Физическая характеристика электрического поля вещества.	Кулон на метр (Кл/м)
Магнитный момент	Физическая характеристика магнитного поля вещества.	Ампер-метр (А·м)

Понимание значения физической величины (ФИ) и правильное ее измерение являются основными аспектами точных физических измерений. Внимательное отношение к деталям, правильная техника и использование подходящих инструментов и приборов с учетом ФИ способсттвуют достижению высокой точности и надежности результатов измерений.

Использование буквы ФИ в единицах измерения

Буква ФИ часто используется в физике для обозначения различных величин и параметров, связанных с магнитными и электрическими явлениями. Магнитное и электрическое поле хорошо описывается с помощью векторов, где направление и величина важны и обозначаются буквой ФИ.

В электричестве и магнетизме буква ФИ часто используется для обозначения электрической и магнитной индукции. Электрическая индукция (ФИ) является векторной величиной и измеряется в единицах Фарадея (Ф), которая равна кулону на метр квадрат. Она характеризует электрическое поле в данной точке пространства.

Магнитная индукция (ФИ) также является векторной величиной и измеряется в единицах тесла (Т), которая равна веберу на метр квадрат. Магнитная индукция определяет магнитное поле в данной точке пространства.

Буква ФИ также используется в измерении силы, в частности, магнитной силы. Магнитная сила определяет взаимодействие магнитных полюсов и измеряется в единицах ампер-метр (А·м).

Использование буквы ФИ в единицах измерения позволяет точно определить и описать различные физические величины, связанные с магнитными и электрическими явлениями. Это обеспечивает более точные и надежные расчеты и эксперименты в области физики.

Классификация[]

Размерные и безразмерные физические величины

• Размерная физическая величина — физическая величина, для определения значения которой нужно применить какую-то единицу измерения этой физической величины. Подавляющее большинство физических величин являются размерными.
• Безразмерная физическая величина — физическая величина, для определения значения которой достаточно только указания её размера. Например, относительная диэлектрическая проницаемость — это безразмерная физическая величина.

Аддитивные и неаддитивные физические величины

• Аддитивная физическая величина — физическая величина, разные значения которой могут быть суммированы, умножены на числовой коэффициент, разделены друг на друга. Например, физическая величина масса — аддитивная физическая величина (в классической механике).
• Неаддитивная физическая величина — физическая величина, для которой суммирование, умножение на числовой коэффициент или деление друг на друга её значений не имеет физического смысла. Например, физическая величина температура — неаддитивная физическая величина.

Экстенсивные и интенсивные физические величины

Физическая величина называется[источник не указан 5368 дней]

• экстенсивной, если величина её значения складывается из величин значений этой физической величины для подсистем, из которых состоит система (например, объём, вес);
• интенсивной, если величина её значения не зависит от размера системы (например, температура, давление).

Некоторые физические величины, такие как момент импульса, площадь, сила, длина, время, не относятся ни к экстенсивным, ни к интенсивным.

От некоторых экстенсивных величин образуются производные величины:

• удельная величина — это величина, делённая на массу (например, удельный объём);
• молярная величина — это величина, делённая на количество вещества (например, молярный объём).

Скалярные, векторные, тензорные величины

В самом общем случае можно сказать, что физическая величина может быть представлена посредством тензора определённого ранга (валентности)[источник не указан 5015 дней].

• Скалярная физическая величина — физическая величина, валентность (ранг) тензора которой равна нулю. Это означает, что данная физическая величина может быть охарактеризована одним числом. Примеры скалярных физических величин:
  • Работа силы;
  • Масса;
  • Энергия;
• Векторная физическая величина — физическая величина, валентность (ранг) тензора которой равна 1. С точки зрения обыденных представлений, как правило, это означает то, что она характеризуется некоторым направлением в пространстве. Такие величины удобно описывать при помощи векторов. С точки зрения линейной алгебры любой вектор — это упорядоченный набор чисел (координат), то есть тензор валентности 1. К векторным физическим величинам относятся как величины, описываемые истинными векторами, так и псевдовекторами[источник не указан 5015 дней] — величинами, изменяющими знак при замене ориентации системы координат на противоположную:
  • примеры векторных физических величин:
    • сила;
    • скорость;
    • импульс;
  • примеры псевдовекторных физических величин:
    • угловая скорость;
    • момент импульса;

• Остальные физические величины описываются тензорами высших валентностей (2 и более), то есть являются тензорными физическими величинами.
  • Многие тензорные величины, ранг тензора которых равен 2 определяются уравнением вида x→=A^y→{\displaystyle {\vec {x}}={\hat {A}}{\vec {y}}}, где x→{\displaystyle \vec{x}} и y→{\displaystyle \vec{y}} — две векторные физические величины, связанные преобразованием A^{\displaystyle \hat{A}}[источник не указан 5015 дней]. Примеры:
    • Тензор инерции;
    • Тензор эффективной массы;
    • Тензор диэлектрической проницаемости.
  • Примеры величин, описываемых тензорами ранга 4

    Тензор упругости.

    :

Особенности движения Фи по окружности

Когда Фи движется по окружности, происходят несколько интересных особенностей. Во-первых, его перемещение происходит с постоянной скоростью и плавно, без резких изменений направления или ускорения. Это связано с тем, что Фи является иррациональным числом, что означает, что его десятичное представление не имеет периода и не может быть точно выражено дробью.

Во-вторых, движение Фи по окружности образует замкнутую траекторию, которая никогда не пересекает себя. Это связано с тем, что Фи обладает свойством самоподобия, что означает, что его значением является отношение длины всей окружности к ее радиусу. Это свойство обеспечивает равномерное распределение Фи по окружности.

Также стоит отметить, что движение Фи по окружности может быть представлено с помощью таблицы. В такой таблице можно отразить изменение координат Фи на окружности в зависимости от времени. Это позволяет визуально представить особенности движения Фи и проанализировать его закономерности.

Время	Угловая координата Фи	Координаты на окружности (x, y)
(r, 0)
1	1	(x1, y1)
2	2	(x2, y2)
…	…	…

Таким образом, движение Фи по окружности обладает уникальными математическими свойствами, которые делают его интересным объектом исследования. Изучение этих особенностей помогает нам лучше понять математические закономерности и их применение в различных областях науки и техники.

Фи — важная характеристика электрических систем

Фи определяет, насколько активная или реактивная энергия перетекает через цепь. Если фи равно нулю, то ток и напряжение синфазны и система работает в режиме активной энергии, например, при питании основных электрических нагрузок. Если фи не равно нулю, то ток и напряжение имеют разность фаз, и система работает в режиме реактивной энергии, которая требуется для работы индуктивных или емкостных компонентов электрической цепи.

Фи может быть положительным или отрицательным, в зависимости от того, сдвигается ли ток вперед или назад относительно напряжения. Положительное фи указывает на поглощение реактивной энергии, тогда как отрицательное фи означает отдачу реактивной энергии обратно в источник.

Знание значения фи позволяет электротехническим специалистам эффективно проектировать и управлять электрическими системами. Например, при проектировании переключателей, реле или регуляторов напряжения учитывается значение фи, чтобы обеспечить правильное взаимодействие этих компонентов с другими элементами цепи.

Измерение фи выполняется специальными приборами, такими как фазовращательные приборы или анализаторы мощности. Эти приборы позволяют определить точное значение фи и использовать его для анализа и управления электрическими системами.

Применение физических законов в технологиях

Физические законы имеют огромное значение в различных областях технологий. Они позволяют предсказывать и объяснять поведение физических систем, а также создавать новые технологические решения.

Одной из важных областей применения физических законов является механика. Законы Ньютона позволяют точно расчитывать движение твердых тел и применяются при разработке автомобилей, самолетов и других транспортных средств. Также, законы механики используются при проектировании и строительстве мостов, зданий и других инженерных сооружений.

Законы термодинамики также имеют важное применение в технологиях. Они определяют эффективность и возможности работы различных двигателей, таких как паровые, внутреннего сгорания и турбинные

Кроме того, законы термодинамики используются в процессе кондиционирования воздуха, холодильных системах, энергетике и других областях.

Электромагнетизм является еще одной областью, где физические законы используются широко. Законы Максвелла описывают электромагнитные поля и их взаимодействие с частицами. Это позволяет создавать различные электрические и электронные устройства, такие как компьютеры, телефоны, телевизоры и многие другие. Также, законы Максвелла применяются в радиосвязи, управлении энергией и других областях технологий.

Квантовая механика и физика элементарных частиц также находят применение в современных технологиях. Они используются в разработке полупроводниковой электроники и квантовых компьютеров, лазеров, атомных электростанций и других инновационных технологий.

Таким образом, физические законы являются фундаментальными основами различных технологий. Они позволяют предсказывать и управлять физическими процессами, что делает их неотъемлемой частью современного мира.

Закон сохранения энергии для гармонических колебаний

Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.

Рассмотрим его на примере математического маятника.

• Когда маятник отклоняют на высоту h, его потенциальная энергия максимальна.
• Когда маятник опускается, потенциальная энергия переходит в кинетическую. Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

Измерение дельта фи: в чем измеряется?

Наиболее распространенным методом измерения дельта фи является использование цифровых осциллографов и фазометров. Цифровые осциллографы позволяют наблюдать и анализировать временные диаграммы сигналов, измерять их фазовые характеристики. Фазометры, в свою очередь, используются для прямого измерения разности фаз между сигналами.

При измерении дельта фи могут использоваться также специализированные приборы, такие как интерферометры, спектроанализаторы и другие. Интерферометры позволяют измерять разность фаз между интерферирующими сигналами с высокой точностью. Спектроанализаторы предназначены для анализа спектра сигналов и определения их фазовых характеристик.

Для более точных и точных измерений дельта фи может использоваться также схема измерительного моста, основанная на принципе сравнения фаз.

Метод измерения	Принцип работы
Цифровой осциллограф	Измерение фазовых характеристик сигналов на основе временных диаграмм
Фазометр	Прямое измерение разности фаз между сигналами
Интерферометр	Измерение разности фаз между интерферирующими сигналами с высокой точностью
Спектроанализатор	Анализ спектра сигналов и определение их фазовых характеристик
Измерительный мост	Сравнение фаз для получения точных и точных измерений

Измерение дельта фи является важным компонентом в многих областях физики, таких как оптика, электроника, радиотехника и другие. Величина дельта фи может сильно влиять на результаты измерений и работу систем, поэтому ее измерение и контроль являются неотъемлемой частью многих экспериментов и исследований.

Вопрос-ответ:

Что такое фи в физике?

В физике фи — это обозначение для физической величины, которая обычно описывает поток чего-либо через поверхность. Например, фи может быть потоком электрического поля через поверхность или потоком магнитного поля через контур.

Как фи влияет на наш мир?

Фи позволяет нам описывать и предсказывать поведение различных процессов и физических явлений в нашем мире. Благодаря измерению и анализу фи, мы можем понять, как электрические и магнитные поля взаимодействуют с материей и друг с другом, и как они влияют на поведение зарядов и токов.

Чему равен фи в различных физических явлениях?

Значение фи зависит от конкретной ситуации и связано с физическими величинами и геометрией системы. Например, фи электрического поля через поверхность равно интегралу от плотности электрического поля по площади поверхности. В случае потока магнитного поля через контур фи равно произведению магнитного поля на площадь контура.

Можете ли вы привести примеры использования фи в реальной жизни?

Конечно! Фи встречается во многих аспектах нашей жизни. Например, фи используется при расчете магнитного потока в электромагнитах, которые применяются в электротехнике и машиностроении. Также фи используется при измерении электрической мощности, где оно представляет поток мощности через поверхность. И это только некоторые примеры использования фи.

Как фи связано с законами электромагнетизма?

Фи является одной из главных концепций законов электромагнетизма. Например, закон Фарадея, который гласит, что изменение магнитного потока через контур индуцирует электродвижущую силу, описывает взаимосвязь между фи и электрическими явлениями. Также фи используется при расчете электрического поля с помощью закона Гаусса, где фи является основой для определения электрического потенциала и поля.

Что такое фи в физике?

Фи в физике обычно обозначает величину потока, то есть количество чего-либо, проходящего через определенную площадку за единицу времени.

Физические величины и развитие технологий

Физические величины играют важную роль в развитии технологий. Они помогают нам описывать и измерять физические процессы, что является основой для создания новых технологий и улучшения существующих.

Одним из примеров использования физических величин в технологиях является электричество. Физическая величина — сила тока — позволяет нам измерять электрический поток, что является основой для разработки и производства электрических приборов. Используя эту величину, мы можем создавать и улучшать электрические схемы, микрочипы и другие электронные компоненты, которые стали неотъемлемой частью нашей повседневной жизни.

Еще одним примером является лазерная технология. Физическая величина — длина волны — играет важную роль в создании и настройке лазерных систем. Измеряя эту величину, мы можем контролировать и управлять лазерным излучением, что позволяет нам использовать лазеры в различных сферах, таких как наука, медицина, производство и коммуникации.

Физические величины также играют ключевую роль в разработке и производстве материалов. Например, физическая величина — температура плавления — позволяет нам определить, при какой температуре материал начинает терять свою прочность и становиться жидким. Зная эту величину, мы можем разрабатывать и производить материалы с определенными свойствами, которые могут быть использованы в различных отраслях, включая строительство, авиацию и электронику.

В целом, физические величины являются незаменимыми инструментами в развитии технологий. Они позволяют нам измерять и описывать физические явления, что является основой для создания новых технологий и улучшения существующих. Использование физических величин в технологиях позволяет нам повышать эффективность процессов, минимизировать риски и улучшать качество продукции, что способствует развитию общества и повышению уровня жизни.

Физический смысл фи

Фи (φ) в физике обычно означает угол или фазу и имеет свой физический смысл в разных контекстах.

Например, в теории колебаний и волн фи обычно используется для обозначения фазового угла колебания. Он показывает, насколько сдвинуто колебание относительно начальной точки. Если две колеблющиеся системы имеют одинаковое значение фи, то они находятся в фазе и колеблются синхронно друг с другом.

В оптике фи может быть использовано для обозначения фазы световой волны

Фаза света относительно точки наблюдения определяет положение световой волны в своем колебательном цикле и имеет важное значение при изучении интерференции и дифракции света

Кроме того, фи может также означать фазу в контексте электрических и магнитных полей, где показывает относительную фазу между двумя взаимодействующими полями.

Смысл фи в физике

В физике понятие «фи» обозначает фийту, единицу измерения магнитного потока. Магнитный поток представляет собой меру того количества магнитных силовых линий, которые проникают через поверхность. Фи измеряется в единицах Вебер (Вб).

Магнитный поток играет важную роль в различных областях физики, таких как электромагнетизм, магнитные материалы и теория поля. Он позволяет описывать взаимодействия между магнитными полями и проводниками, а также исследовать электромагнитные явления во вселенной.

Одним из примеров использования магнитного потока является закон Фарадея, который гласит, что электродвижущая сила, возникающая в замкнутом проводнике, пропорциональна скорости изменения магнитного потока, пронизывающего этот проводник.

Единица измерения	Обозначение	Величина
Вебер	Вб	Количество магнитного потока

Таким образом, фи в физике имеет важное значение для понимания и описания магнитных явлений и их взаимодействий с другими физическими величинами

На что влияет фи в физике

Влияние фи в физике зависит от контекста использования. Например, фи может использоваться для измерения угла поворота. В этом случае, значение фи определяет, насколько точка или объект повернут относительно других объектов или оси. Углы могут быть измерены в радианах (2π радиана составляют полный оборот) или в градусах (360 градусов составляют полный оборот).

Фи также используется для обозначения потока. Поток (флюкс) — это количество частиц, энергии или информации, проходящих через определенную поверхность. Значение фи в этом контексте определяет, сколько частиц, энергии или информации проходит сквозь данную поверхность за определенное время. Формула для вычисления потока включает фи, площадь поверхности и скорость частицы.

Кроме того, фи может быть использовано для представления электрического потенциала. Электрический потенциал показывает силу, с которой заряженная частица будет взаимодействовать с другими заряженными частицами в электрическом поле. Значение фи определяет разность потенциалов между двумя точками. Чем больше разница потенциалов, тем сильнее электрическое поле и сильнее будет влиять на заряженную частицу.

Зачем нужно знать фи в физике

Знание фи в физике играет важную роль, так как это позволяет нам понять и описать вращение объектов и явления, которые связаны с этим движением. Фи представляет собой угол, который измеряется в радианах и показывает, насколько объект или система повернулись относительно начального положения.

Знание фи позволяет нам решать различные задачи в физике, связанные с поворотом. Например, при изучении механики твердого тела, мы можем использовать фи для описания вращательного движения объектов, таких как колесо, волчок или планета. Фи также используется в электродинамике при рассмотрении электрических и магнитных полей и их взаимодействия с заряженными частицами.

Зная фи, мы можем определить угловую скорость объекта, его угловое ускорение и момент инерции. Эти величины являются ключевыми в физике и используются для описания различных процессов и явлений, таких как крутящий момент двигателя, стабилизация вращения спутника или характеристики ротационных молекул.

Кроме того, фи является важной величиной при решении задач о динамике системы объектов. Зная фи каждого объекта, мы можем рассчитать их относительное положение, скорость, ускорение и силу взаимодействия

В общем, знание фи в физике помогает нам понять и описать различные физические явления, связанные с вращением, а также решать задачи по этой теме. Фи играет важную роль в многих областях физики и позволяет нам более глубоко и точно изучать и объяснять окружающий нас мир.

Превращение энергии при гармонических колебаниях

Чтобы описать превращения энергии при гармонических колебаниях, условимся, что силой трения будем пренебрегать. Для описания обратимся к рисунку ниже.

Точке О на рисунке соответствует положение равновесия шарика. Если его оттянуть на расстояние x_max, равное амплитуде, пружина получит потенциальную энергию, которая примет в этом положении максимальное значение, равное:

W p m a x = k x 2 m a x 2 . .

Когда шарик отпускают, возникает сила упругости, под действием которой шарик устремляется влево. По мере уменьшения расстояния между точкой максимального отклонения и положением равновесия уменьшается и потенциальная энергия. Но в это время увеличивается кинетическая энергия шарика. Когда шарик проходит через положение равновесия в первый раз, его потенциальная энергия становится равной нулю, а кинетическая энергия обретает максимальное значение (скорость в этот момент времени тоже максимальна):

W k m a x = m v 2 m a x 2 . .

После прохождения точки О расстояние между шариком и положением равновесия снова увеличивается, и потенциальная энергия растет. Кинетическая же энергия при этом уменьшается. А в крайнем положении слева она становится равной нулю, в то время как потенциальная энергия снова примет максимальное значение.

Так как мы условились пренебрегать трением, данную колебательную систему можно считать изолированной. Тогда в ней должен соблюдаться закон сохранения энергии. Согласно ему, полная механическая энергия системы равна:

W = W p + W k = k x 2 x 2 . . + m v 2 x 2 . . = k x 2 m a x 2 . . = m v 2 m a x 2 . .

В действительности свободные колебания всегда затухают, так как в колебательной системе действует сила трения. И часть механической энергии рассеивается в виде тепла. Пример графика затухающих колебаний выглядит следующим образом:

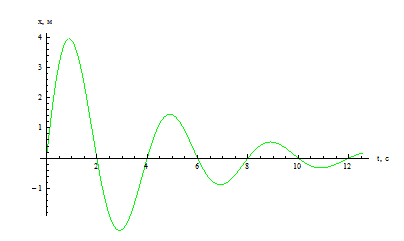
Пример №2. Груз, прикрепленный к пружине, колеблется на горизонтальном гладком стержне. Найдите отношение кинетической энергии груза к его потенциальной энергии системы в момент, когда груз находится в точке, расположенной посередине между крайним положением и положением равновесия.

Так как груз находится посередине между крайним положением и положением равновесия, его координата равна половине амплитуды:

В это время потенциальная энергия груза будет равна:

W p = k x 2 2 . . = k ( x m a x 2 . . ) 2 2 . . = k x 2 m a x 8 . .

Согласно закону сохранения энергии, кинетическая энергия в это время равна:

Полная механическая энергия системы равна максимальной потенциальной энергии:

W = W p m a x = k x 2 m a x 2 . .

Тогда кинетическая энергия равна:

W k = k x 2 m a x 2 . . − k x 2 m a x 8 . .

Следовательно, отношение кинетической энергии к потенциальной будет выглядеть так:

W k W p . . = k x 2 m a x 2 . . − k x 2 m a x 8 . . k x 2 m a x 8 . . . . = k x 2 m a x 2 . . 8 k x 2 m a x . . − 1 = 4 − 1 = 3

Практическое применение Фи в движении по окружности

Фи может быть использован для создания эффективных алгоритмов, позволяющих роботам двигаться по окружностям с большой точностью и стабильностью

Это особенно важно при выполнении задач, требующих точного позиционирования или манипулирования объектами на окружности

Например, в промышленной робототехнике Фи может использоваться для управления движением роботов с шаговыми двигателями. При задании Фи в качестве целевой точки, робот может двигаться по заданной траектории с высокой точностью, минимизируя ошибку позиционирования и обеспечивая стабильное движение.

Также, Фи может быть применено в автомобильной промышленности для управления системами автоматической парковки или системами управления стабилизацией при движении по криволинейной траектории. Зная Фи в каждый момент времени, автомобиль может рассчитать оптимальные углы поворота колес и точное управление движением, что способствует безопасности и комфорту вождения.

В области виртуальной и дополненной реальности, Фи может использоваться для симуляции движения по окружностям, что позволяет создавать реалистичные и плавные анимации и эффекты взаимодействия.

Практическое применение Фи в движении по окружности имеет широкий спектр возможностей и продолжает развиваться вместе с развитием технологий и роботизации. Знание и использование данной концепции позволяет создавать более эффективные и точные системы движения, что может быть полезно во многих областях человеческой деятельности.